OMGosh - somebody shoot me...
...and when someone breaks our wings, we simply continue to fly...on a broomstick.
We are flexible.
Darlene
For other senses of this term, see escape velocity (disambiguation).
In physics, escape velocity is the speed where the kinetic energy of an object is equal to the magnitude of its gravitational potential energy, as calculated by the equation,
It is commonly described as the speed needed to "break free" from a gravitational field (without any additional impulse) and is theoretical, totally neglecting atmospheric friction. The term escape velocity can be considered a misnomer because it is actually a speed rather than a velocity, i.e. it specifies how fast the object must move but the direction of movement is irrelevant, unless "downward." In more technical terms, escape velocity is a scalar (and not a vector).
Escape velocity gives a minimum delta-v budget for rockets when no benefit can be obtained from the speeds of other bodies for a particular mission; but it neglects losses such as air drag and gravity drag. However in some cases it can be improved upon, for example, by use of gravitational slingshots.
Contents[hide] |
[edit] Overview
The phenomenon of escape velocity is a consequence of conservation of energy. For an object with a given total energy, which is moving subject to conservative forces (such as a static gravity field) it is only possible for the object to reach combinations of places and speeds which have that total energy; and places which have a higher potential energy than this cannot be reached at all.
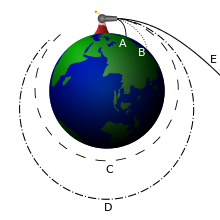
For a given gravitational potential energy at a given position, the escape velocity is the minimum speed an object without propulsion needs to have sufficient energy to be able to "escape" from the gravity, i.e. so that gravity will never manage to pull it back. For the sake of simplicity, unless stated otherwise, we will assume that the scenario we are dealing with is that an object is attempting to escape from a uniform spherical planet by moving straight up (along a radial line away from the center of the planet), and that the only significant force acting on the moving object is the planet's gravity.
Escape velocity is actually a speed (not a velocity) because it does not specify a direction: no matter what the direction of travel is, the object can escape the gravitational field (though its path may intersect the earth). The simplest way of deriving the formula for escape velocity is to use conservation of energy. Imagine that a spaceship of mass m is at a distance r from the center of mass of the planet, whose mass is M. Its initial speed is equal to its escape velocity, ve. At its final state, it will be an infinite distance away from the planet, and its speed will be negligibly small and assumed to be 0. Kinetic energy K and gravitational potential energy Ug are the only types of energy that we will deal with, so by the conservation of 'energy',
Kƒ = 0 because final velocity is zero, and Ugƒ = 0 because its final distance is infinity, so
Defined a little more formally, "escape velocity" is the initial speed required to go from an initial point in a gravitational potential field to infinity with a residual velocity of zero, with all speeds and velocities measured with respect to the field. Additionally, the escape velocity at a point in space is equal to the speed that an object would have if it started at rest from an infinite distance and was pulled by gravity to that point. In common usage, the initial point is on the surface of a planet or moon. On the surface of the Earth, the escape velocity is about 11.2 kilometers per second (~6.96 mi/s), which is approximately 34 times the speed of sound (mach 34) and at least 10 times the speed of a rifle bullet. However, at 9,000 km altitude in "space", it is slightly less than 7.1 km/s.
The escape velocity relative to the surface of a rotating body depends on direction in which the escaping body travels. For example, as the Earth's rotational velocity is 465 m/s at the equator, a rocket launched tangentially from the Earth's equator to the east requires an initial velocity of about 10.735 km/s relative to Earth to escape whereas a rocket launched tangentially from the Earth's equator to the west requires an initial velocity of about 11.665 km/s relative to Earth. The surface velocity decreases with the cosine of the geographic latitude, so space launch facilities are often located as close to the equator as feasible, e.g. the American Cape Canaveral (latitude 28°28' N) and the French Guiana Space Centre (latitude 5°14' N).
That amount is the integral of the expression above:
That is how much kinetic energy the object of mass m needs in order to escape. The kinetic energy of an object of mass m moving at speed v is (1/2)mv2. Thus we need
The factor m cancels out, and solving for v we get
If we take the radius of the Earth to be r = 6400 kilometers and the acceleration of gravity at the surface to be g = 9.8 m/s2, we get
This is just a bit over 11 kilometers per second, or a bit under 7 miles per second, as Isaac Newton calculated.
[edit] Derivation using G and M
Let G be the gravitational constant and let M be the mass of the earth or other body to be escaped.
By applying the chain rule, we get:
Because 
Since we want escape velocity
 and
and 







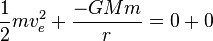
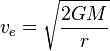

![\begin{align}
\int_r^\infty gm \left(\frac{r}{s}\right)^2 \, ds
& = gmr^2 \int_r^\infty s^{-2}\,ds
= gmr^2 \left[-s^{-1}\right]_{s:=r}^{s:=\infty} \\
& = gmr^2\left(0-(-r^{-1})\right)=gmr.
\end{align}](http://upload.wikimedia.org/math/4/5/a/45a05fc05991c8dd772c24310d8d7a86.png)













